Differential privacy for bandits and RL

Recently, I have been interested in privacy protection in online decision-making, with a focus on bandits and reinforcement learning (RL). In this post, I would like to point out some subtlety in the definition of differential privacy (DP) for bandits and RL.

Let us start with the simple multi-armed bandit learning protocol.

In practice, the reward feedback is often sensitive (e.g., medical treatment). Thus, most existing papers on private bandits adapt the standard central model of DP to bandit learning as follows.

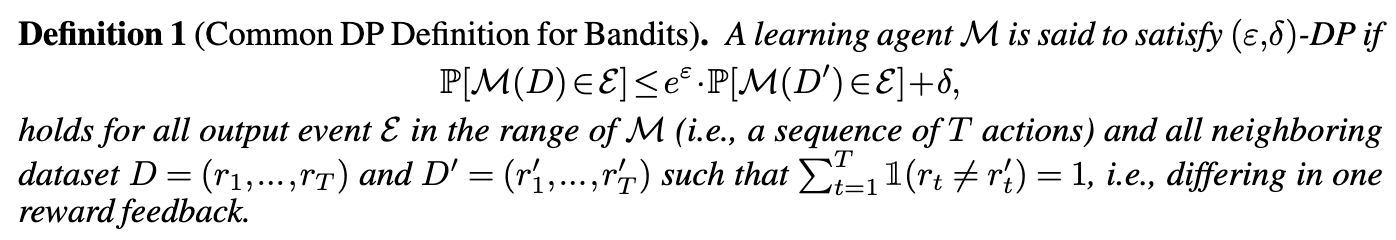
However, this definition is not satisfying and also problematic in some sense:

• First, what we really want to protect is the identity of the user rather than a simple reward feedback at a particular round. More specifically, we want to guarantee that any adversary who observes the agent’s prescribed actions cannot infer too much about the sensitive information of any user. The sensitive information here could be whether the user has participated in the learning process or not, as well as her entire preference (reward feedback) for all possible prescribed actions – which defines the “type” of the user.

• Second, the above definition implicitly assumes that the learning agent can be fed with two reward sequences that only differ in one round. However, this is somewhat problematic since the change of reward feedback in round \(t\), will naturally change the agent’s algorithm for future rounds, hence different reward feedback after round \(t\).

To address the above issues, a more proper definition is to adopt users as the dataset, i.e., \(D = (u_1,\ldots, u_T)\). Technically speaking, we say two users are identical if they have the same preference (reward feedback) for all possible actions, i.e., they are the same “type”. Then, we have the following definition.

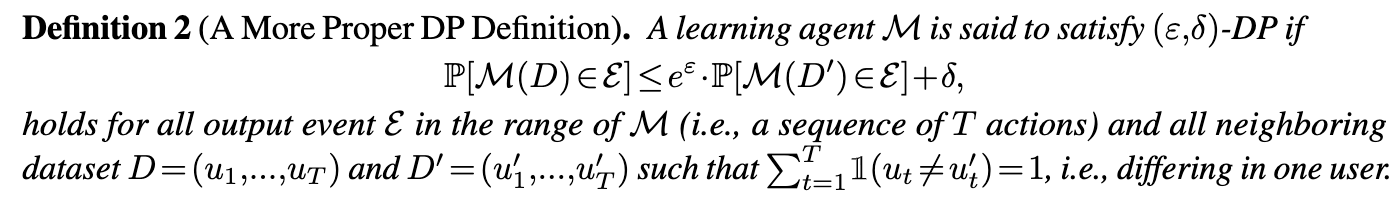
By definition, we can see that using the users as the dataset directly protects the identity of each user, hence resolving the first issue above. Moreover, now we can replace one user while fixing all other users the same, hence fixing the second issue above.

The above definition is not the so-called user-level DP. It is still an item-level DP. Let’s compare it with standard item-level DP for private SGD (e.g., [BST’14]), where each data point is (feature, label), which will generate feedback (e.g., gradient) at a particular parameter weight vector. This is similar to bandit learning when the dataset consists of users. That is, each data point is a user (i.e., the entire reward preference), which will generate feedback (e.g., reward \(r_t\)) upon receiving a particular action. This in turn justifies that Def. 2 is a proper and more natural one. In fact, private online learning with full information (rather than bandit feedback) also considers the entire loss vector as the datapoint in \(\mathcal{D}\) (see [ST’13]), which shares the same spirit as Def. 2.

Now, one can easily see that the second definition is stronger than the first one in general. Then, one may wonder whether the current private bandit algorithm that guarantees DP under Def. 1 still provides DP guarantee under Def. 2. In particular, if one user \(u_t\) is changed, it will not only affect the reward feedback at round \(t\), but it will also change future feedback. Will this cause problems? Note that under Def.1, it assumes that there is only one feedback that is different.

It turns out that it will NOT be a problem. That is, existing privacy mechanism in private bandit learning papers still provides DP guarantee under Def.2 thanks to adaptive composition of DP. This property is in fact already used in private SGD or private online learning to address a similar issue, where changing one sample or loss vector will impact all follow-up gradient feedback (e.g., see the proof of Theorem 3 in [ST’13] where the authors explicitly mentioned how to address it using adaptive composition while other papers essentially use the same idea as it is kind of folklore). The key intuition is that for a given output event \(\mathcal{E}\), one computes its probability using chain rule of conditional probability. This conditioning on the same action removes the possible correlation. The same intuition also applies to the computation of privacy loss random variable, which is widely used in establishing adaptive composition result. Note that adaptive composition also holds for other types of DP, e.g., zero-concentrated DP [BS’16] and Renyi DP [Mironov’17]

For episodic reinforcement learning (RL), one can easily follow the same fashion by considering dataset that consists of users instead of particular observations. Now, the “type” of a user is identified by the state and reward she would give to all possible \(A^H\) actions, where \(A\) is the number of actions and \(H\) is the length of one episode. This is exactly the definition adopted in [VBKW’20] (where when \(H=1\) and number of states \(S=1\), it reduces to Def. 2 above for MAB). Note that in RL, the output sequence needs to be slightly modified by considering joint DP, i.e., removing the requirement for her own action. Otherwise, one has to incur linear regret (which is also easy to understand since now action is personalized with the state).

Summary

• One commonly used DP definition for bandits is not satisfying.

• A more proper one is to consider dataset that consists of users (rather than the particular observation)

• Thanks to adaptive composition of DP, the existing privacy mechanism still provides formal privacy guarantee under the new definition.

One more thing…

If you are also interested in private bandit or RL, please take a look at our recent publications (with Sayak Ray Chowdhury) 😊. In particular, see our recent ICLR’23 paper for private bandit¹, ICML’22 for private contextual bandits and AAAI’22 for private RL. All of them provide a comprehensive study of different trust models of DP, e.g., central, local and distributed DP. In the future, I may also try to give more details on each paper.

THE END

Now, it’s time to take a break by appreciating the masterpiece of Monet.

Cliff Walk at Pourville

courtesy of www.Claude-Monet.com